Floyd-Warshall(플로이드 와샬) 알고리즘

Floyd-Warshall Algorithm

 

- 그래프에서 모든 정점 사이의 최단 거리를 구하기 위한 알고리즘

- 다익스트라 알고리즘을 모든 정점에서 수행한 것과 같은 알고리즘이지만 플로이드 와샬 알고리즘은 구현이 간단하다.

- 음수 가중치에 대한 처리가 어려운 다익스트라 알고리즘에 비해 플로이드 와샬 알고리즘은 사이클이 없는 경우 음수 가중치 처리가 가능하다.

 

 

Floyd-Warshall Complexity

 

- 단순히 반복문 3개를 vertex만큼 돌기 때문에 O(V^3)의 시간 복잡도를 갖는다.

- 특정 정점에서 특정 정점까지의 경로를 저장해나가며 구한 경로를 이용해 새로운 최단 경로를 찾는 DP방식으로 수행된다. 그러므로 2차원 배열이 필요하므로 O(V^2)의 공간 복잡도를 갖는다.

V : 정점의 갯수

 

 

Floyd-Warshall Process

 

- 단방향 그래프

- 어떤 특정 정점을 거쳤을 때의 경로가 최단이라면 table을 update한다.

- 이전에 구했던 최단 경로를 통해 새로운 최단 경로를 찾는 방식으로 진행된다.

 

Example) Floyd-Warshall

- 단방향 그래프에서의 Floyd-Warshall

 

 

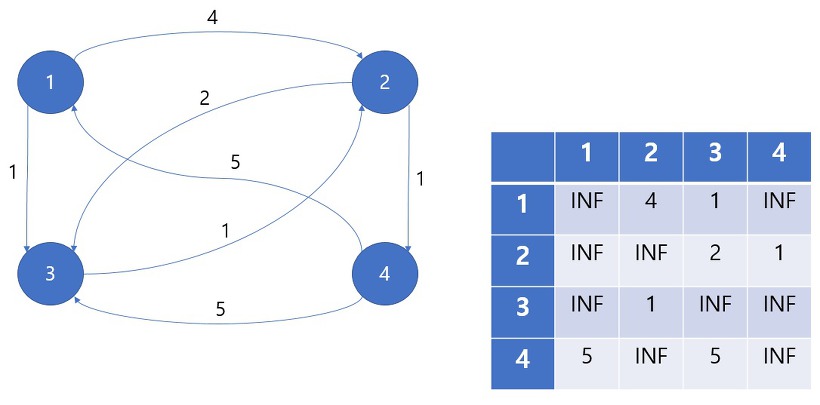
직접 갈 수 있는 vertex가 아니라면 INF(무한대)값으로 초기화하고 정점->정점으로의 경로가 있다면 가중치를 넣고 초기화해줌

 

경유해서 갈 수 있는 최단 경로가 있는 지 확인하기 위해 모든 vertex를 경유 vertex로 설정하여 모든 정점을 탐색해본다.

1번 vertex를 경유할 때의 가중치

1) 4->1, 1->2 : 5+4

   arr[4][2] = min(arr[4][2], arr[4][1]+arr[1][2])

 

 

2번 vertex를 경유할 때의 가중치

1) 1->2, 2->4 : 4+1

   arr[1][4] = min(arr[1][4], arr[1][2]+arr[2][4])

2) 3->2, 2->3 : 1+1

   arr[3][3] = min(arr[3][3], arr[3][2]+arr[2][3])

3) 3->2, 2->4: 1+1

   arr[3][4] = min(arr[3][4], arr[3][2]+arr[2][4])

4) 4->2, 2->4 : 9+1

   arr[4][4] = min(arr[4][4], arr[4][2]+arr[2][4])

 

 

3번 vertex를 경유할 때의 가중치

1) 1->3, 3->2 : 1+1

   arr[1][2] = min(arr[1][2], arr[1][3]+arr[3][2])

2) 1->3, 3->4 : 1+2

   arr[1][4] = min(arr[1][4], arr[1][3]+arr[3][4])

3) 2->3, 3->2 : 2+1

   arr[2][2] = min(arr[2][2], arr[2][3]+arr[3][2])

4) 4->3, 3->2 : 5+1

   arr[4][2] = min(arr[4][2], arr[4][3]+arr[3][2])

5) 4->3, 3->4 : 5+2

   arr[4][4] = min(arr[4][4], arr[4][3]+arr[3][4])

 

 

4번 vertex를 경유할 때의 가중치

1) 1->4, 4->1 : 3+5

   arr[1][1] = min(arr[1][1], arr[1][4]+arr[4][1])

2) 2->4, 4->1 : 1+5

   arr[2][1] = min(arr[2][1], arr[2][4]+arr[4][1])

3) 3->4, 4->1 : 2+5

   arr[3][1] = min(arr[3][1], arr[3][4]+arr[4][1])

 

이러한 방식으로 특정 경로간의 최단 경로를 구하며 점점 먼 경로까지의 최단 경로를 이전에 구한 최단 경로를 이용해 채워나간다.